Projects

Digital Twin for Rapid Damage Evaluation of Bridge Structures

Summary

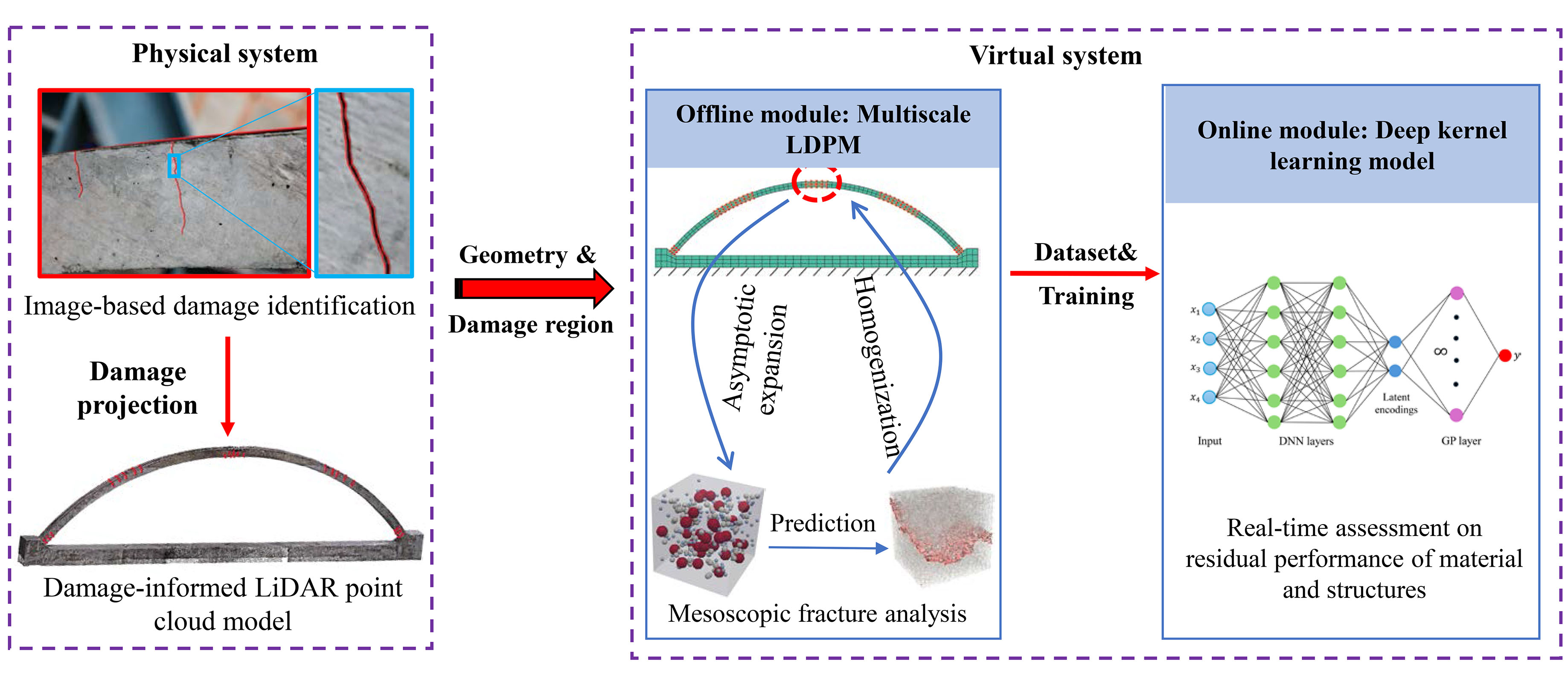
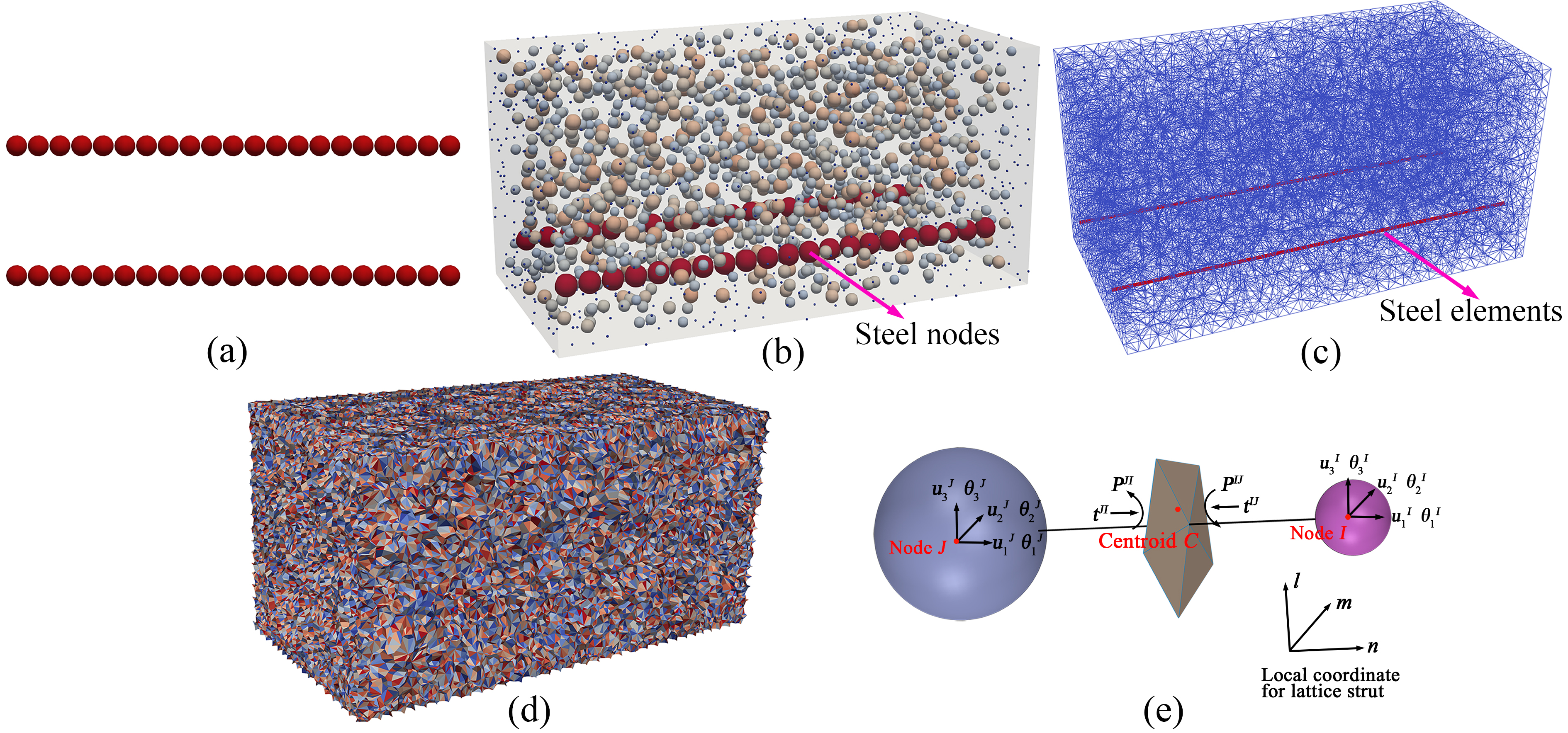
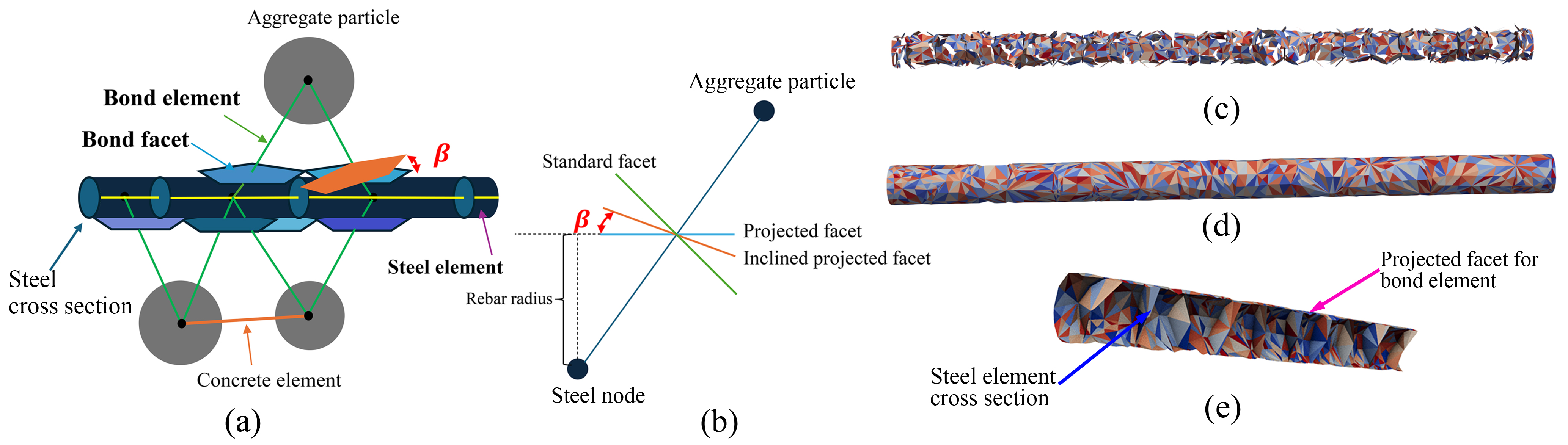
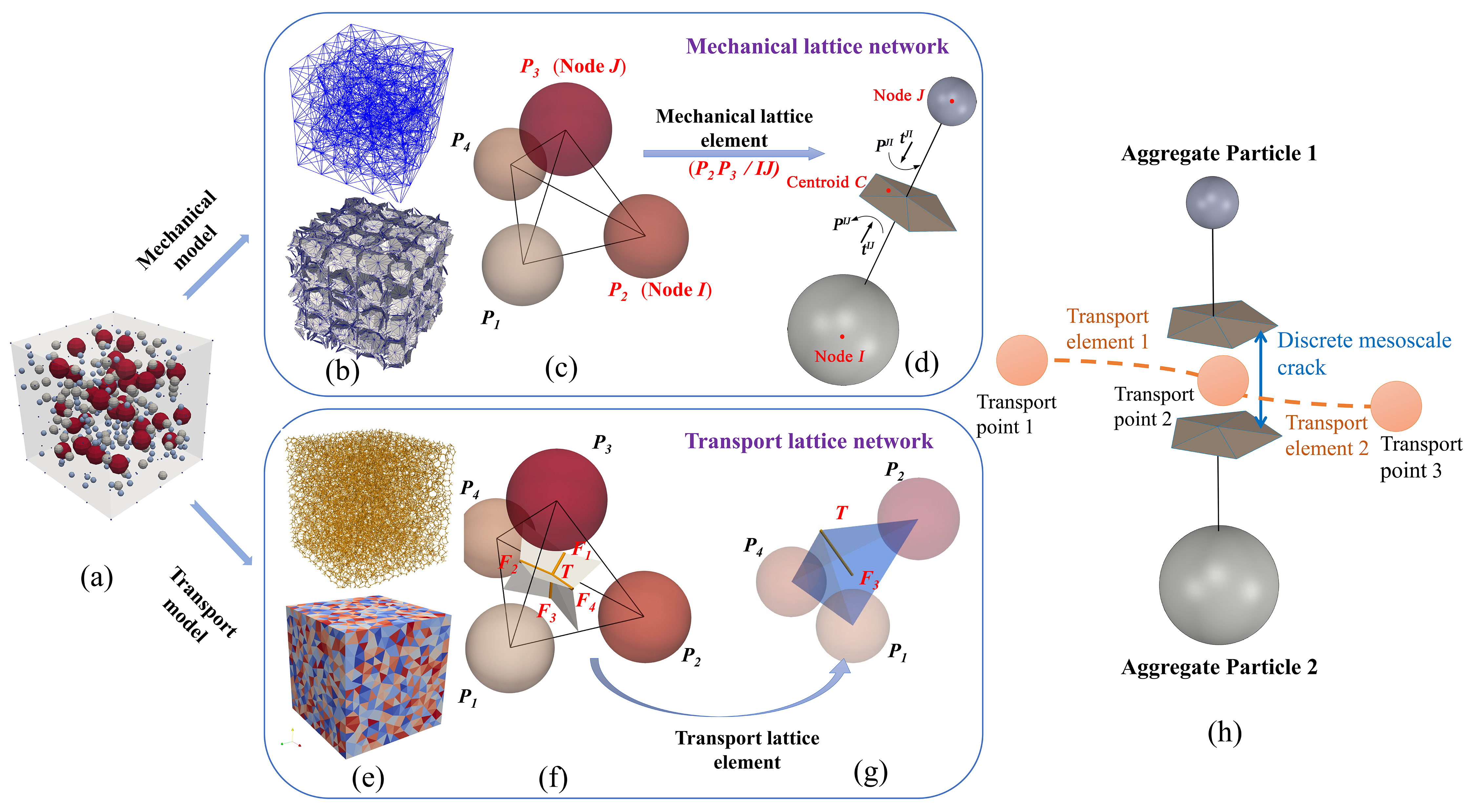
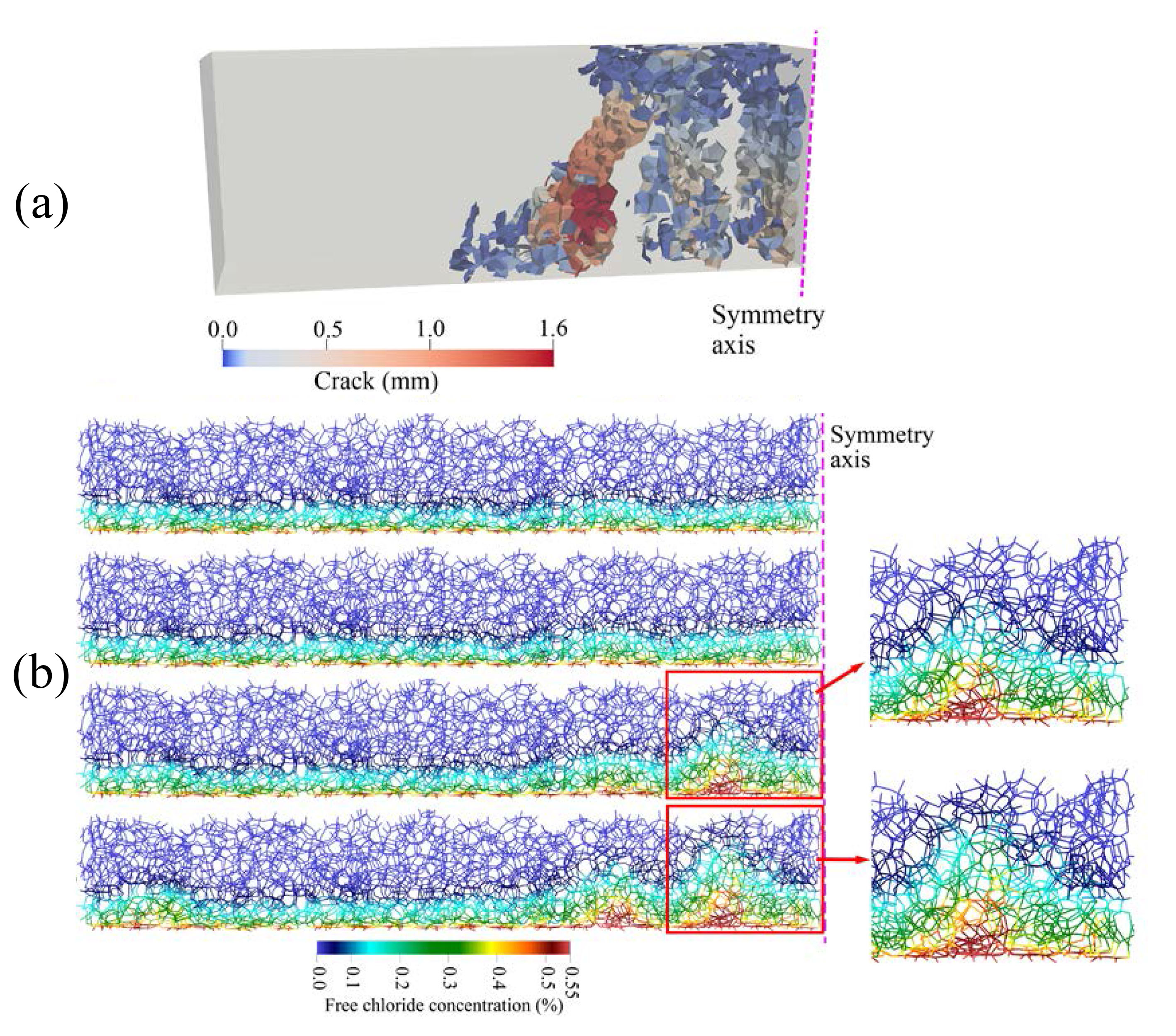
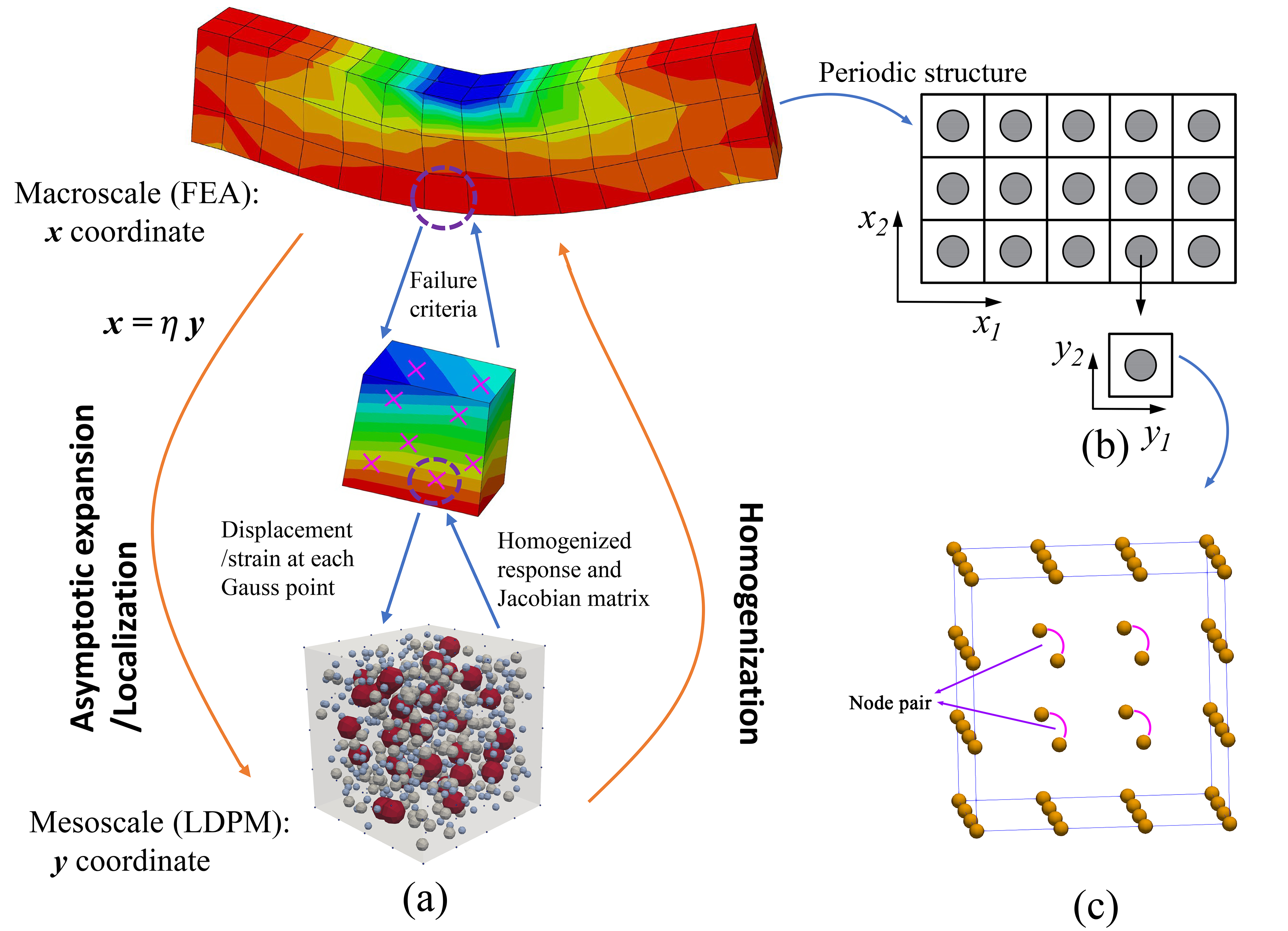
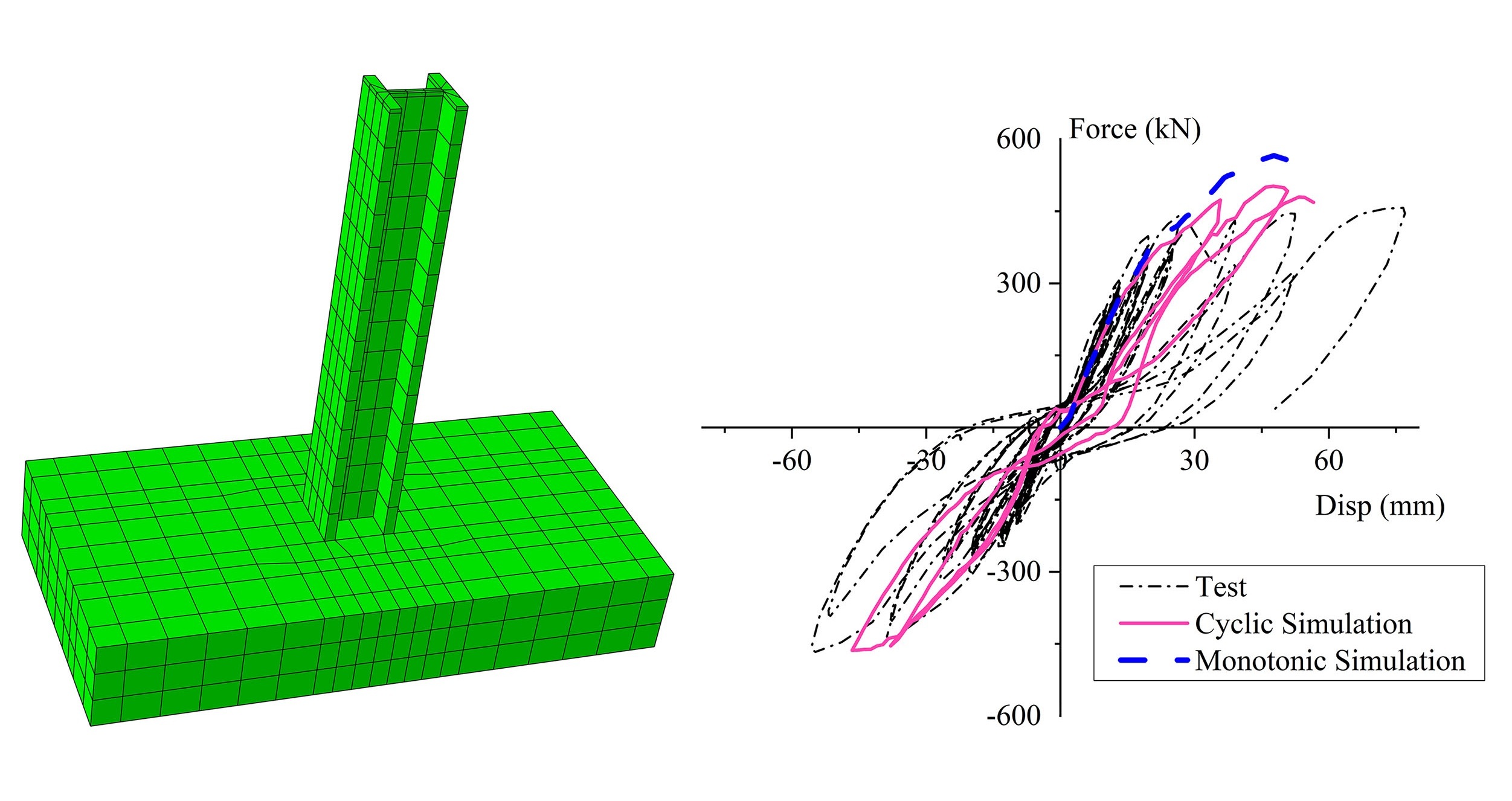
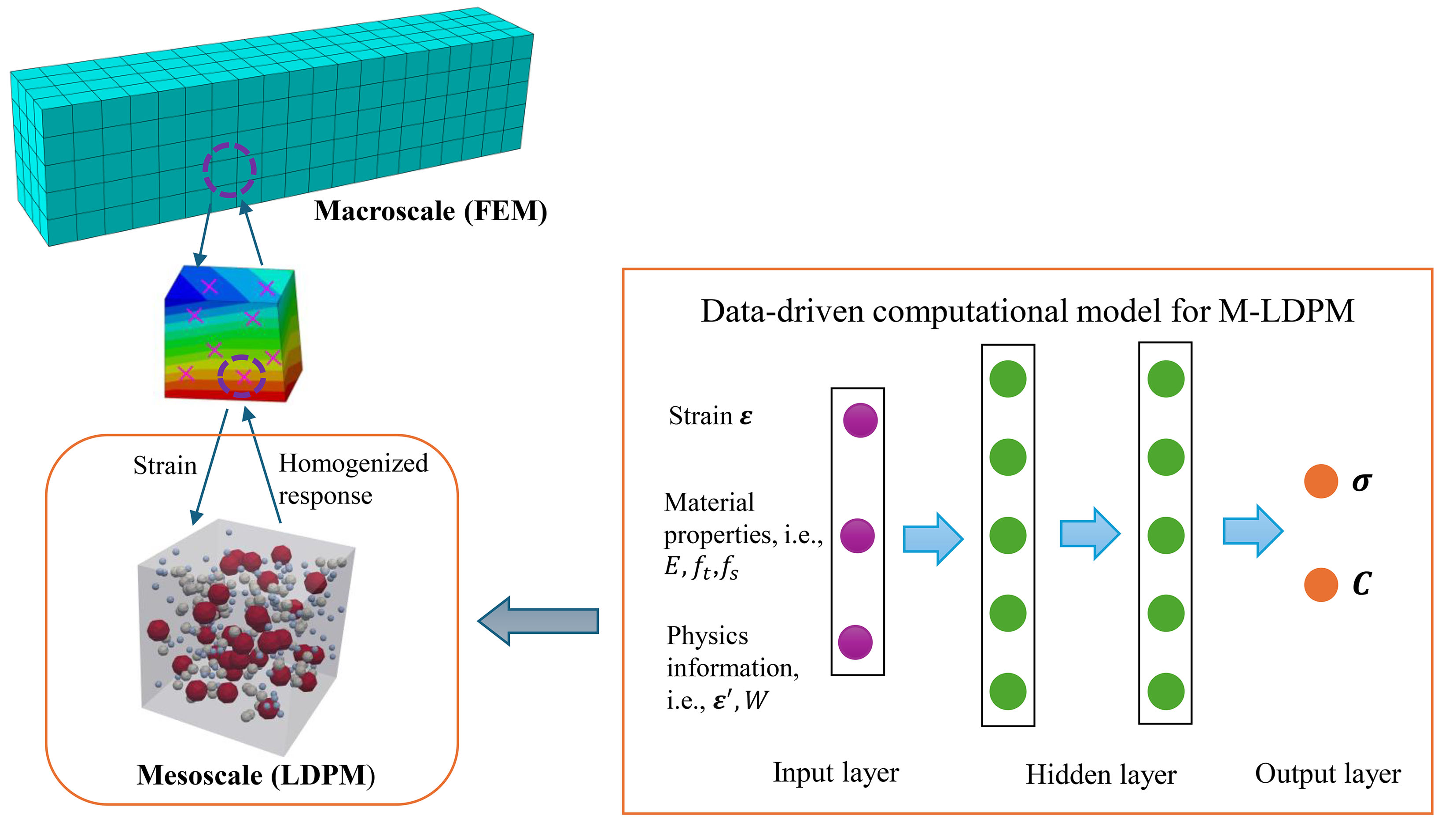
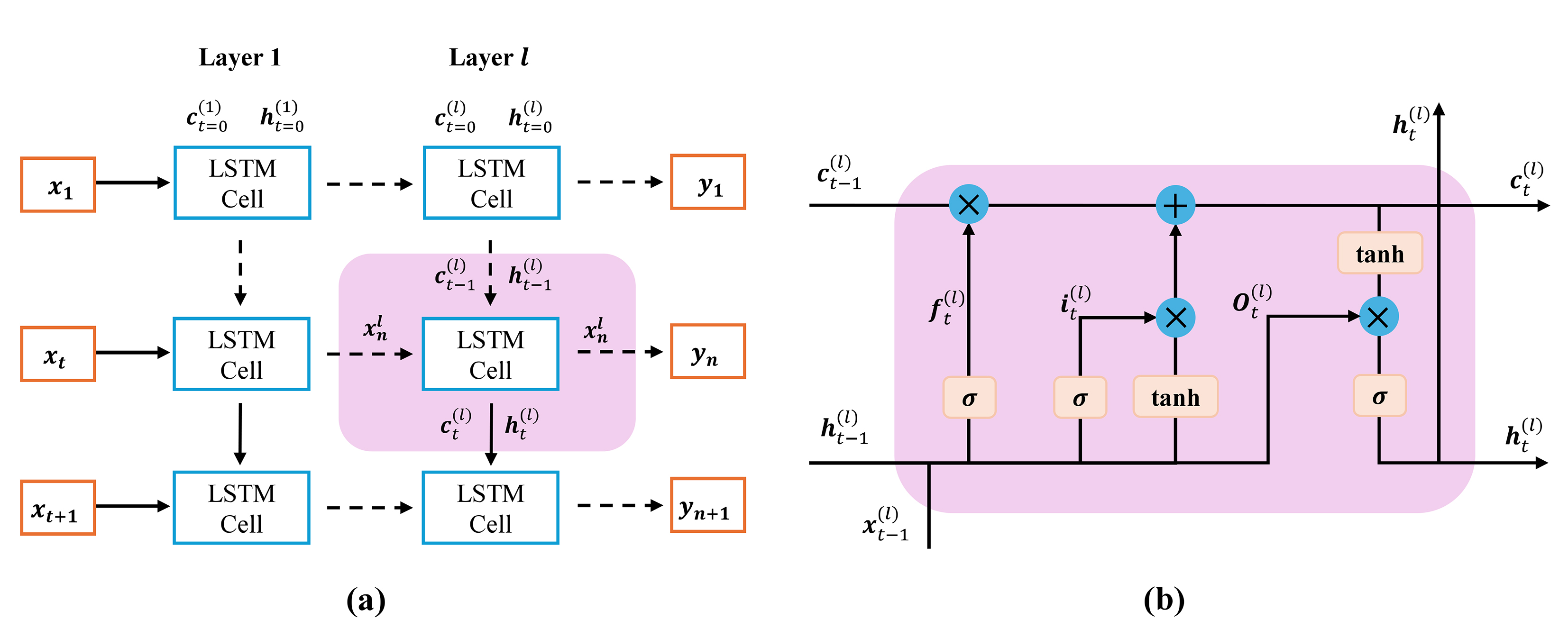
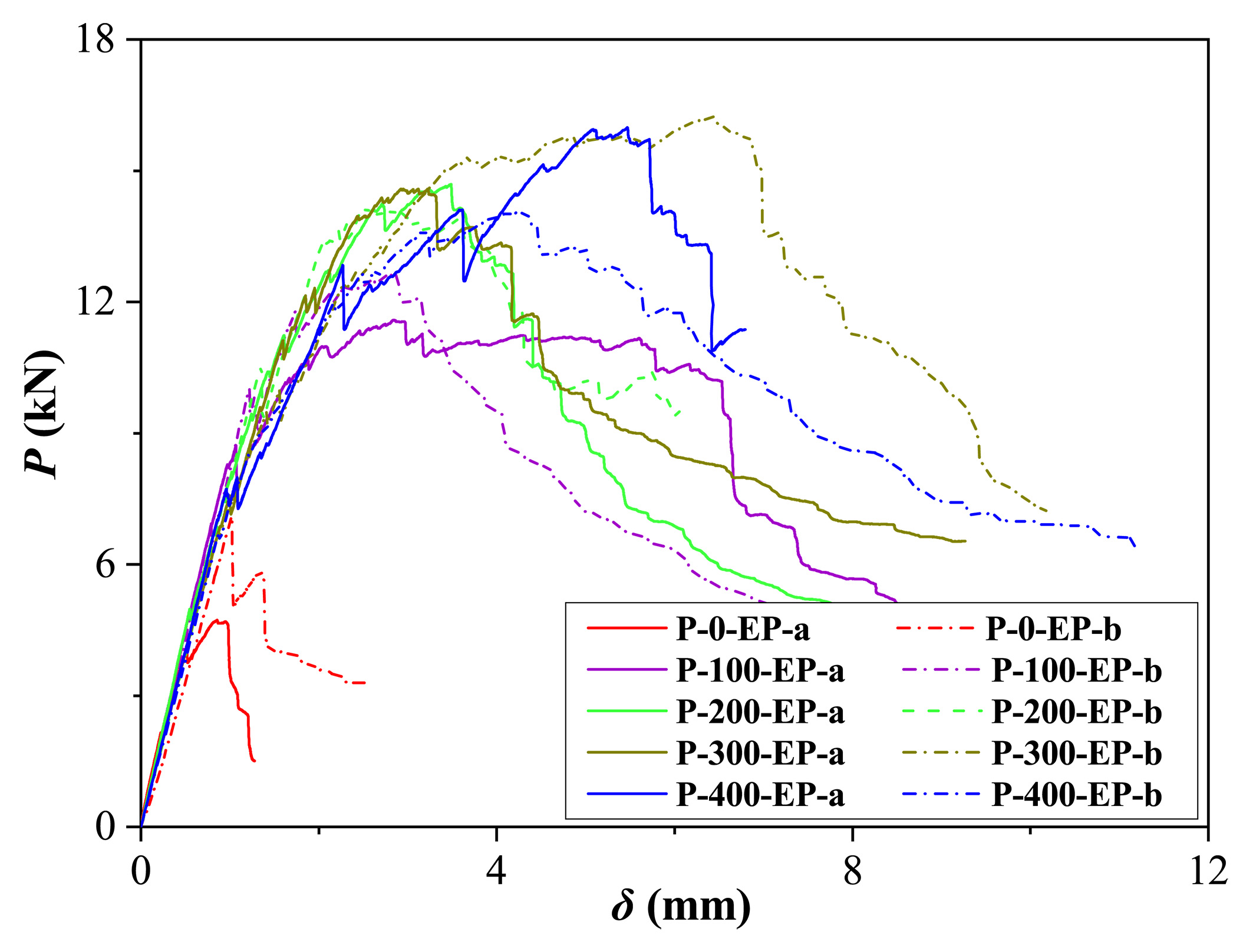
A novel DT framework is proposed, developed, and validated for Reinforced Concrete (RC) bridges by integrating remote sensing technology, Multiscale Lattice Discrete Particle Modeling (M-LDPM), and machine learning technology. In the physical entity, this proposed DT framework combines local sensor data with global LiDAR point clouds and photogrammetric crack detection to achieve accurate deformation tracking and damage zone identification. In the virtual system, an online-offline strategy is used to rapidly and accurately estimate the damage conditions of RC structures. In the offline phase, the high-fidelity M-LDPM method is employed to generate a comprehensive dataset of structural responses under various damage scenarios, which is then used to train a deep kernel learning surrogate model. During the online phase, the trained surrogate facilitates rapid estimation of residual material properties in the damaged structures while quantifying predictive uncertainty.

Key Results

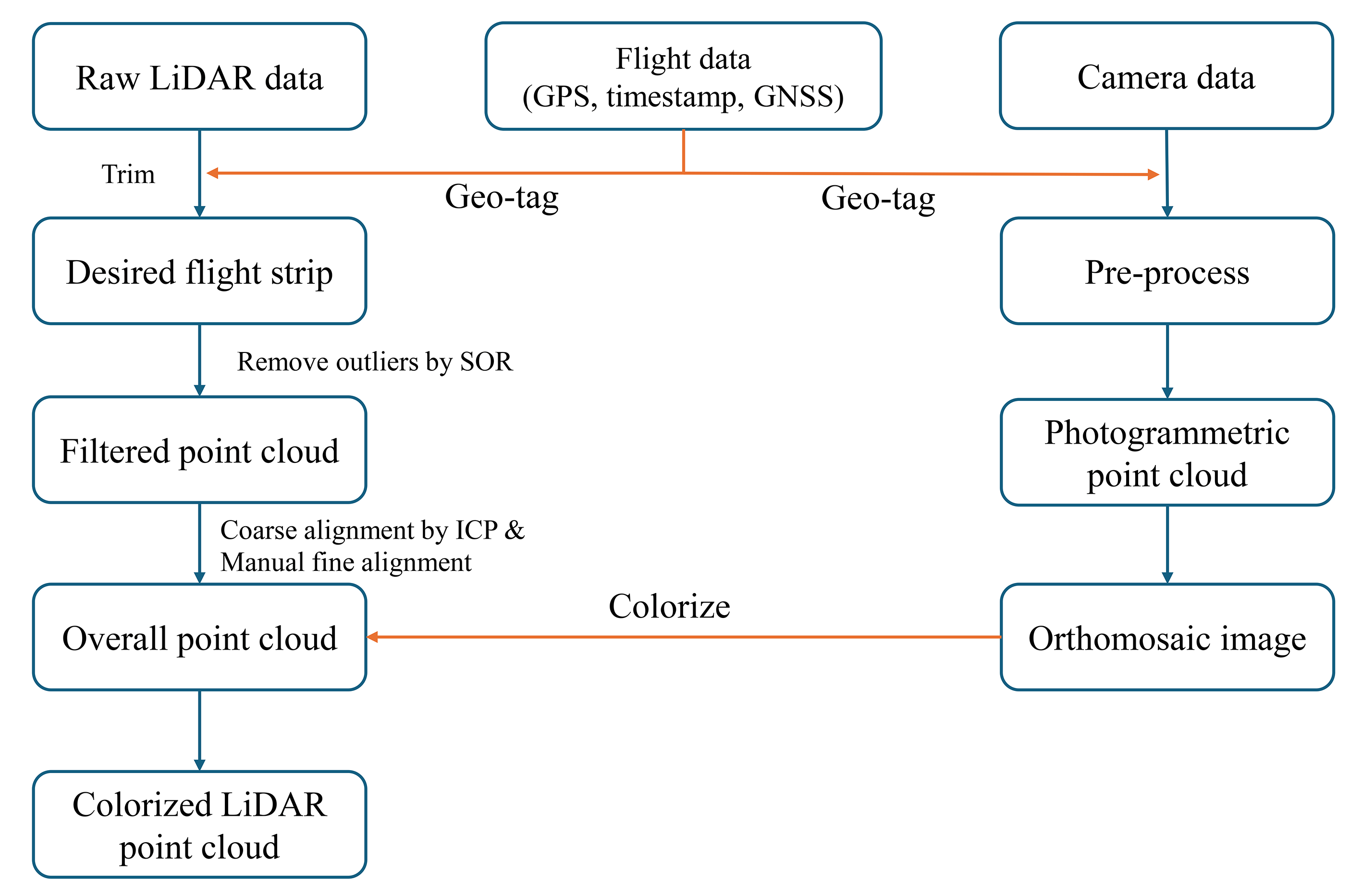
• LiDAR enables twin model generation and captures global deformation of structures.
• Photogrammetry facilitates damage identification and segmentation in twin models.
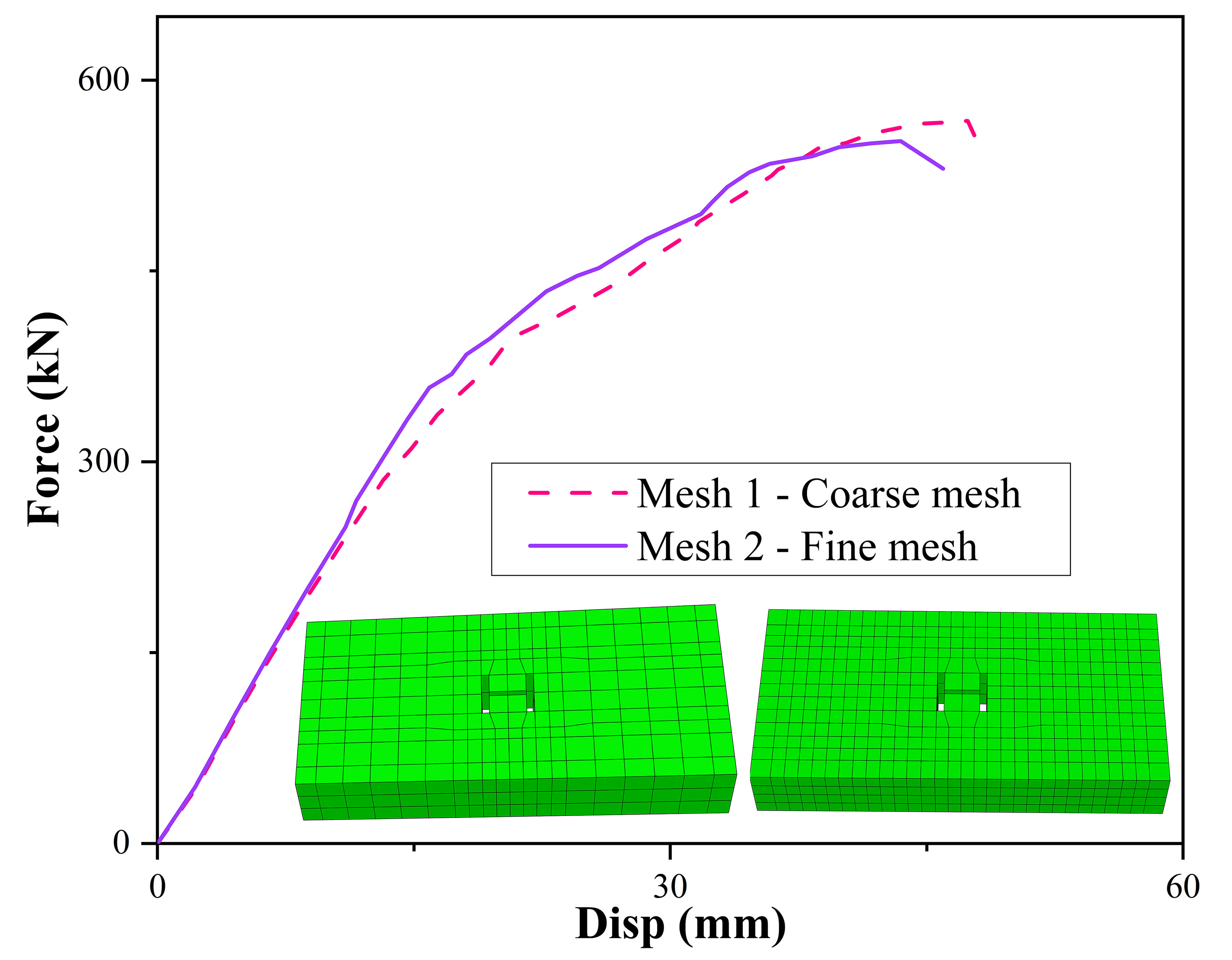
• M-LDPM accurately captures nonlinear structural response.
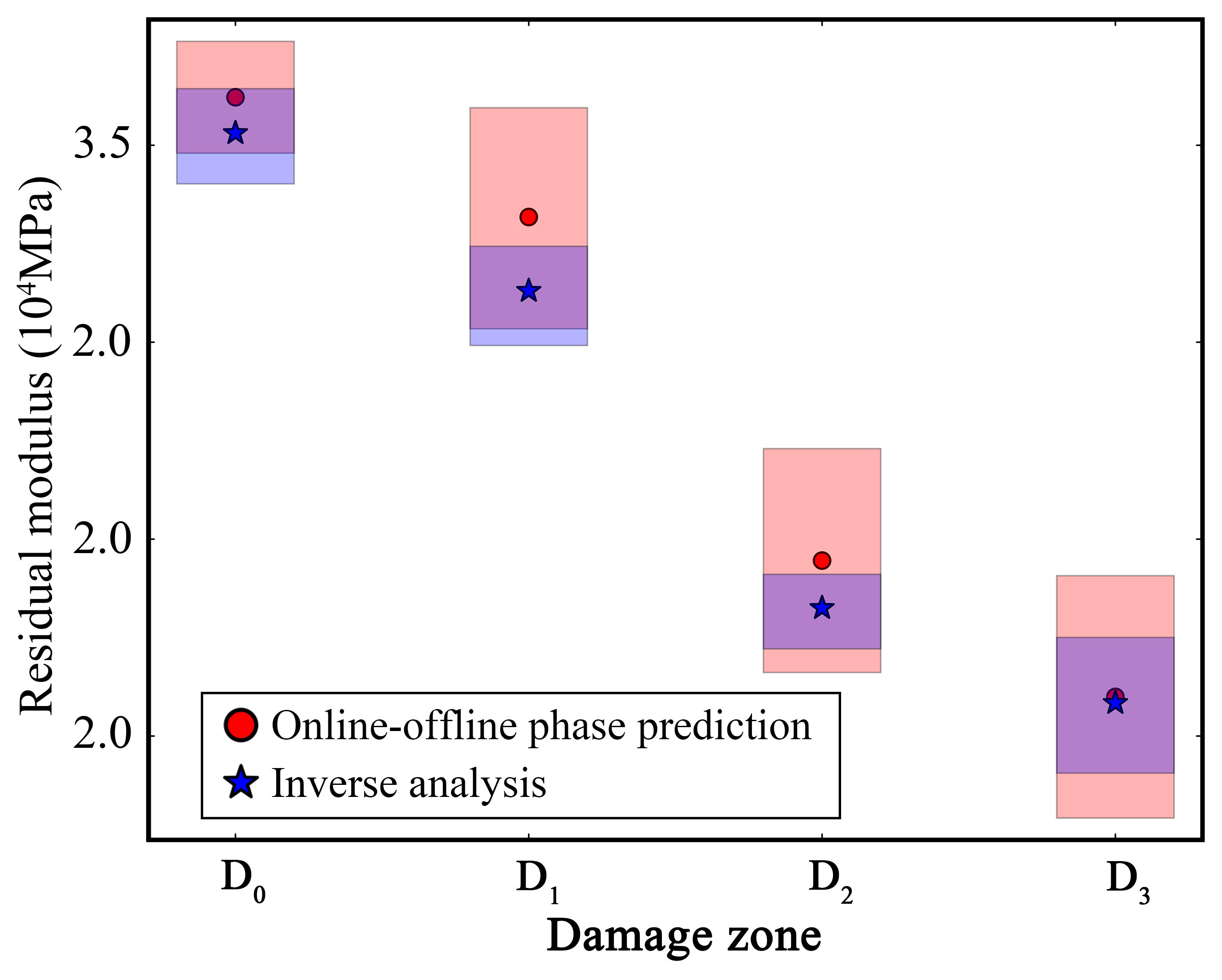
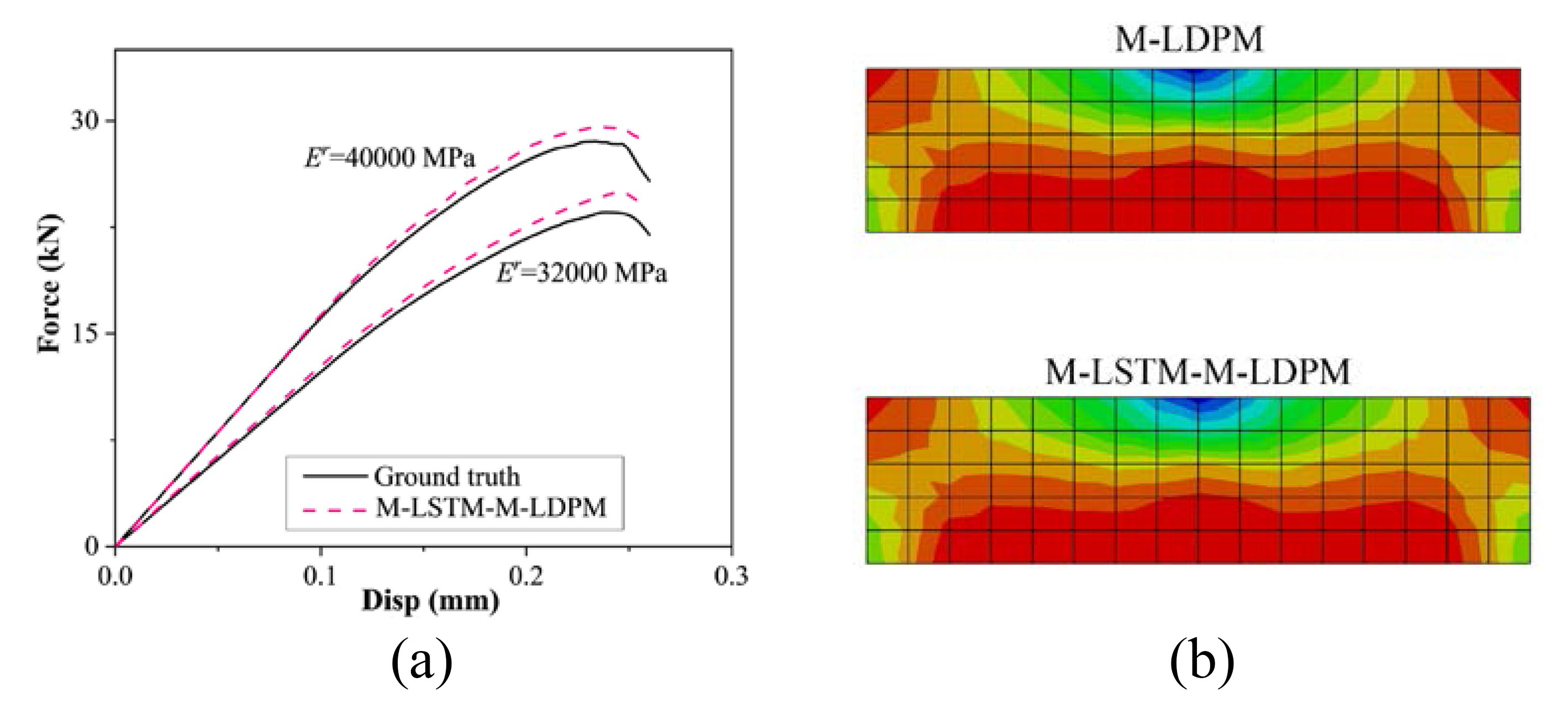
• Deep kernel learning surrogate model achieves 1~2s damage assessment with high accuracy.
  
  

LiDAR–RGB Fusion Framework for Intelligent Monitoring of Bridge Construction

Summary

A 4D UAV-based monitoring framework integrating LiDAR and RGB photogrammetry is proposed and validated through the Fern Hollow Bridge reconstruction case study. The approach demonstrates how LiDAR-RGB data fusion can provide accurate, continuous, and safe monitoring during bridge construction, enhancing quality assurance and control (QA/QC). The resulting fused point clouds can serve as the digital foundation for generating and updating Digital Twin models, bridging sensing technology with virtual simulation and decision support.

Key Results

• Develop a UAV-mounted LiDAR-RGB sensing system capable of generating dense (≥ 500 pts/m²) and accurate 3D point clouds throughout construction phases.
• LiDAR-RGB fusion provides centimeter-level accuracy for global and local geometry, outperforming photogrammetry in both integrity and precision of reconstructions.
• Demonstrate the potential of LiDAR-RGB fusion as a digital foundation for QA/QC and digital twin development for bridge construction.
  
  

Lattice Discrete Particle Model for Reinforced Concrete Structures

Summary

A novel Lattice Discrete Particle Model (LDPM) framework is proposed for reinforced concrete (RC) structures, with a special focus on accurately simulating the bond–slip interaction between steel reinforcement and concrete at the mesoscale. The framework introduces a high-fidelity reinforcement geometry generation method, enabling realistic modeling of steel–concrete interfaces. The bond elements incorporate the effects of rib inclination angles through a rotating-angle formulation, allowing the model to capture the mechanical interlocking effect that governs bond strength and slip. Furthermore, new bond stress–strain and compressive constitutive laws are developed to describe the complex nonlinear interaction at the steel-concrete interface.

Key Results

• Bond–slip behavior is accurately captured for both unconfined and confined concrete cylinders.
• Rotating-angle formulation effectively simulates the influence of rib inclination and mechanical interlock on bond strength and ductility.
• Pull-out simulations show that confinement suppresses splitting failure, producing localized pull-out mode consistent with experiments.
• Four-point bending simulations on beams with lap splices capture experimental force–deflection curves, force–slip relationships, cracking patterns, and fracture modes.
  
  

Coupled Multiphysics LDPM for Mass Transport in Concrete Members under Long-Term Loading

Summary

A coupled mechanical-mass transport LDPM is proposed to quantify the influence of cracking on water and chloride transport in concrete under both short- and long-term loading. The framework proposed dual lattice networks, i.e., one for mechanical response and another for transport, to directly map local crack information onto transport elements. The approach integrates convective and diffusive transport mechanisms, considers creep-induced cracking under sustained loads, and introduces an exponential relationship between local diffusivity and crack width to capture the effects of both macro- and micro-cracks.

Key Results

• Develop a 3D dual-lattice topology that aligns transport paths with mechanical cracks for realistic mesoscale coupling.
• Incorporate creep behavior in long-term loading simulations, revealing its significant effect on chloride ingress.
• Propose a new diffusivity–crack-width relationship capable of accounting for micro- and macro-cracks.
• Accurately capture water absorption and chloride diffusion curves in tension, compression, and bending.
• Demonstrate that relative water content and creep effects substantially accelerate chloride penetration and rebar corrosion.
  
  

Density-Driven Damage Mechanics

Summary

A Regularized Density-Driven Damage Mechanics (D3M) model is developed to simulate the progressive damage evolution and failure mechanisms in cementitious composites. The model introduces a physics-based concept in which local density change is directly linked to the degradation of material stiffness, offering a measurable and physically meaningful indicator of damage. A novel energy-based regularization scheme eliminates mesh dependency and ensures objective results across different spatial resolutions. The three-phase mesoscale representation (aggregate, mortar, and ITZ) enables realistic tracking of micro-to-macro damage transition under tension, compression, and bending.

Key Results

• Damage evolution is governed by local density reduction, naturally representing stiffness degradation and crack coalescence during loading.
• The energy-based regularization stabilizes strain localization and ensures consistent damage propagation patterns independent of mesh size.
• The model accurately captures the initiation and propagation of microcracks into macroscopic fractures in uniaxial and bending tests.
• Accurately capture uniaxial tensile and compressive responses, including realistic compression-to-tension strength ratios.
  
  

Physics-Based Multiscale LDPM

Summary

A physics-based multiscale LDPM (M-LDPM) framework is proposed for high-fidelity simulation of RC structures. The model establishes a quantitative link between macroscopic structural behavior and mesoscale fracture mechanisms, allowing representation of damage initiation, propagation, and failure evolution in RC structures. A novel energy-based regularization strategy, grounded in crack-band theory, eliminates mesh sensitivity and reduces computational cost while preserving objectivity of the damage process.

Key Results

• Develop a regularized multiscale LDPM that ensures mesh-objective fracture energy dissipation across varying lattice resolutions.
• Accurately capture pull-out and cyclic hysteretic curves of large-scale structures, including asymmetric degradation and stiffness loss.
• Demonstrate consistent damage localization patterns and realistic stress transfer at steel–concrete interfaces.
• Significantly reduce computational cost when compared to full-order LDPM.
  
  

Data-Driven Based M-LDPM

Summary

A data-driven multiscale modeling framework that integrates theLDPM with Multi-Long Short-Term Memory (M-LSTM) neural networks to efficiently capture the nonlinear and path-dependent behavior of concrete. The proposed M-LSTM-M-LDPM replaces computationally intensive mesoscale simulations with deep-learning surrogates trained on LDPM-generated datasets. Two dedicated LSTM modules independently predict the stress tensor and material tangent matrix, enabling accurate and stable simulations of both intact and damaged concrete.

Key Results

• Develop a M-LSTM surrogate capable of learning the nonlinear, history-dependent response of LDPM representative volume elements.
• Introduce a reduced-order damage representation linking residual material parameters to the degraded modulus, enabling efficient learning of multiscale degradation.
• Achieve 4× speedup and 2.7× lower memory usage compared with the standard M-LDPM, while maintaining accuracy within 2% of full-order simulations.
• Demonstrate excellent agreement in force-displacement and stress fields between the data-driven model and M-LDPM across multiple damage scenarios.
  
  

  

Large-Scale Test on Composite Steel-Concrete Bridge

Summary

Composite box-girders with corrugated steel webs (CBGCSWs) shows superior performance over traditional concrete box-girder, with benefits such as lighter self-weight and non-cracking of webs. However, the use of corrugated steel webs leads to a significant reduction in torsional stiffness (about 60–70%) compared with conventional concrete bridges. In this context, six large-scale CBGCSW specimens are tested under pure torsion to investigate the influence of key parameters on cracking torque, stiffness degradation, and failure progression. Furthermore, finite element models (FEMs) are developed and validated against the experimental results to further investigate the influence of web geometry, concrete strength, and reinforcement configurations.

Key Results

• Single-box multi-cell (SBMC-CBGCSWs) specimens show ductile behavior, with failure caused by concrete spalling. The diagonal crack angle ranged from 32°–42°, while web buckling occurred at 23°–27°.
• Three distinct stages, crack initiation, stable crack propagation, and localized spalling failure, are observed, with cracks primarily concentrates near web–slab junctions.
• Unequal web spacing increases torsional stiffness and strength.
• Inner corrugated steel webs (CSWs) contribute little to the cracking torque but sustained load after the outer CSWs yielded, improving post-yield strength.
• FEM accurately captures the experimental torque-twist response, shear-strain distribution, and failure mode, validating the model.
  
  

Theoretical Model Development and Validation

Summary

To accurately predict the nonlinear torsional response of CBGCSWs with varying cell configurations and reinforcement layouts, a unified rotating-angle softened truss model (URA-STMT) is developed. The proposed model is extensively validated against the experimental results obtained from this study and other publication, demonstrating excellent agreement in predicting cracking torque, stiffness degradation, and ultimate torsional capacity.

Key Results

• New three-stage average stress coefficients for concrete strut is proposed.
• The influence of prestressing on concrete element is incorporated.
• A new two-stage shear strain relationship between steels webs and concrete slabs is proposed.
• A shear strain relationship between inner and outside CSWs for estimating the torsional contribution of inner CSW.
  
  

Structural Rehabilitation using CFRP

Summary

This project experimentally and theoretically investigates the repair and performance recovery of damaged composite bridge structures using Carbon Fiber-Reinforced Polymer (CFRP). Four large-scale damaged composite bridge specimens are tested under torsional loading to quantify the effects of CFRP on stiffness restoration, cracking, and ultimate strength. Furthermore, a rotating-angle softened truss model is developed, incorporating damage coefficients and FRP-confined constitutive laws for degraded concrete materials. The proposed model accurately captures the nonlinear torsional behavior and strength recovery of repaired members, providing a predictive framework for optimizing CFRP-based rehabilitation strategies in RC structures.

Key Results

• Conduct large-scale torsional tests on CFRP-repaired damaged composite bridge structures, investigating crack reopening, recovery performance, and failure mode during reloading.
• CFRP-repaired damaged structures improve stiffness by 40–50 % and ultimate capacity by up to 92 % compared with the damaged ones without repair under secondary loading.
• Propose a constitutive model for CFRP-repaired degraded concrete to quantify material and structural nonlinear performance.
• Develop a novel rotating-angle model (RA-STMT-FRP) capable of accurately predicting nonlinear response, failure modes, and FRP strain evolution in CFRP-repaired damaged structures.
  
  

  

GFRP-Strengthened Structural Elements

Summary

This research investigates the mechanical behavior and reinforcement strategy of Glass Fiber-Reinforced Polymer (GFRP) structural elements, focusing on improving the strength and stiffness of Web–Flange Junctions (WFJs), where are the most critical regions prone to premature failure. An extensive experimental campaign is conducted on GFRP I-beams strengthened with externally bonded L-shaped pultruded stiffeners of varying lengths, investigating the role of local reinforcement in delaying delamination and enhancing capacity. Finite element model (FEM) incorporating cohesive zone elements is developed to simulate the mechanical interaction between the epoxy-bonded stiffeners and the base profile.

Key Results

• Reinforcement strategies using bonded GFRP stiffeners for Web–Flange Junctions that increase the ultimate strength by up to 160 % and elastic limit by more than 120 % compared with unreinforced profiles.
• Digital Image Correlation (DIC) mapping reveals progressive damage evolution and confirmed that stiffeners redistributed stresses, producing more ductile response and delayed web–flange separation.
• FEM simulations using 3D cohesive elements accurately captures the experimental force–displacement behavior and DIC displacement fields, validating the modeling approach.